Выплата стипендий 2017

10.06.2020

Задание 1. Составьте электронную таблицу для решения уравнения вида

с анализом дискриминанта и коэффициентов a, b, c. Для обозначения коэффициентов, дискриминанта и корней уравнения применить имена.

Выполнение.

Вид электронной таблицы может иметь следующий вид.

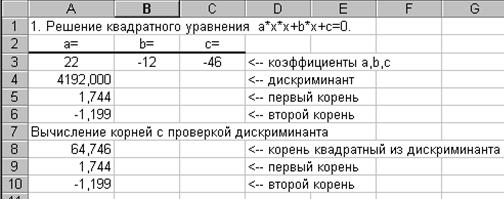Задание 2. Дана таблица с итогами экзаменационной сессии.

Итоги экзаменационной сессии

Составить электронную таблицу, определяющую стипендию по следующему правилу:

По рассчитанному среднему баллу за экзаменационную сессию (s) вычисляется повышающий коэффициент (k), на который затем умножается минимальная стипендия (m).

Повышающий коэффициент вычисляется по правилу:

если 4 £ s < 8, то k=1.2,

если 8 £ s < 10, то k=1.8,

если s= 10, то k=2.0

Если же s<4 или s>10, то стипендия не назначается и поэтому нужно в этом случае коэффициент k вычислять специальным образом, например, присвоить k текст «Неправильные данные»

Выполнение.

1. Составить исходную таблицу:

Итоги экзаменационной сессии

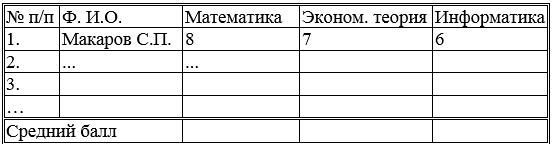
2. Составить электронную таблицу для выплаты стипендий.

· Построить таблицу по образцу

· Графу Ф.И.О. скопировать с исходной таблицы.

· Графы средний балл и стипендия рассчитать по соответствующим формулам с использованием логических функций ЕСЛИ, И, ИЛИ, НЕ.

Выполнение:

1. В начале необходимо внести на лист Excel таблицу согласно образцу, заполнив необходимое количество записей – студентов и их оценок по трем предметам:

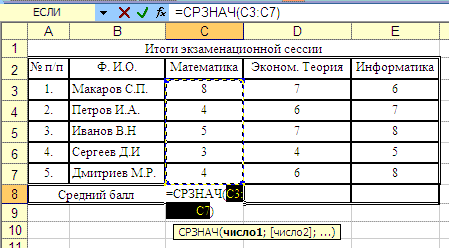
2. Необходимо также заполнить ячейки С8, D8 и E8, в которых с использованием функции СРЗНАЧ() необходимо рассчитать средний балл по каждому из трех предметов.

Оптимально использовать кнопку панели инструментов Автосумма:

Сначала необходимо сделать активной ячейку C8, затем на панели инструментов открыть меню кнопки Автосумма и выбрать функцию Среднее и затем, убедившись, что предложена правильная функция СРЗНАЧ() и правильный диапазон ячеек C3:C7 (в ячейках этого диапазона приведены оценки по предмету Математика всех пяти студентов), нажать клавишу Ввод.

Останется лишь, вновь сделав активной ячейку C8, переместить курсор мыши к ее правому нижнему углу (так, чтобы он выглядел как черный крестик), нажать на левую кнопку мыши и, не отпуская ее, скопировать содержимое в ячейки D8 и E8. В результате получим три средних значения оценок по трем предметам:

3. Далее необходимо подготовить таблицу для расчета стипендий студентов, продублировав их порядковые номерами фамилии (Ф.И.О.), а в качестве трех других заголовков столбцов записать Средний балл, Коэффициент и Стипендия (то есть переменные s, k и m):

4. Затем необходимо заполнить ячейки со средними баллами студентов (столбец Средний балл).

4.1 Вначале необходимо вычислить средний балл по трем предметам первого студента.

Для этого надо сделать активной ячейку С12 (средний балл студента Макарова С.П.) и вызвав окно мастера функций (нажав на кнопку fx), выбрать функцию СРЗНАЧ(), и в качестве исходных данных выбрать диапазон C3:F3(содержащий оценки студента Макарова С.П. по всем трем предметам). В результате в строке формул появится запись СРЗНАЧ(С3:F3):

После нажатия ОК будет подсчитан средний балл студента Макарова С.П. за сессию и я ячейке C12 появится значение 7:

4.2 Остается скопировать введенную формулу в ячейки, соответствующие всем остальным студентам.

Для этого необходимо сделать активной ячейку C12 и подведя к ее правому нижнему углу указатель мыши, нажать левую клавишу мыши и скопировать значения в ячейки С13, С14, С15 и С16. Таким образом, будут подсчитаны средние баллы всех студентов:

5. Затем необходимо вычислить коэффициенты для расчета стипендии согласно правилу в условиях, то есть заполнить соответствующий столбец.

5.1 Вначале вычисляется коэффициент первого студента.

Коэффициент зависит от среднего балла (s) согласно правилу в условиях (см. выше), таким образом, надо последовательно проверить:

— выполняется ли для величины среднего балла первое условие (4 <= s < 8) – в случае выполнения коэффициент равен — 1.2,

— затем – второе условие (8 <= s < 10) – в случае выполнения коэффициент равен — 1.8,

— затем третье условие (s = 10) – в случае выполнения коэффициент равен — 2,

— а в случае невыполнения ни одного из условий необходимо выдать сообщение «неправильные данные”.

Проверка будет осуществляться с использованием нескольких вложенных функций ЕСЛИ(Логическое_ выражение;Значение_если_истина;Значение_если_ложь). Исходными данными этой функции является Логическое выражение (на первом месте) и два значения – а результатом ее выполнения – одно из заданных на втором либо на третьем месте значений, в зависимости от того, равно ли ИСТИНЕ логическое выражение.

Для ввода функции надо сделать активной ячейку D12 (Коэффициент, используемый для расчета стипендии студента Макарова С.П.), и вызвав окно мастера функций (нажав на кнопку fx), выбрать функцию ЕСЛИ():

Вначале введем условия (Логическое выражение) для первого варианта коэффициента (если 4 <= s <8, то k=1,2). – Как сказано выше, в том случае, если средний балл студента больше либо равен 4 но меньше 8, то его коэффициент равен — 1,2. Учитывая, что условия фактически 2 (первое – s больше либо равно 4, второе – s меньше 8 ), нам понадобится еще одна логическая функция – И(), в результате выполнения которой выдается ИСТИНА в том случае, если все ее аргументы (логические выражения т.е. условия) также равны ИСТИНЕ. В данном случае у этой функции будет два аргумента (условия) – выполнение первого условия (4 <= s) и выполнение второго условия (s <8). В случае выполнения обоих коэффициент будет равен 1,2.

Для их записи установим курсор мыши в окно ввода логического выражения функции ЕСЛИ() и запишем И()

после чего установим курсор мыши в окне ввода формул после И перед открывающей скобкой – в результате будет открыто окно ввода аргументов для функции И():

Введем аргументы – в качестве первого – С12>=4, в качестве второго С12<8:

и вернемся ко вводу аргументов функции ЕСЛИ(), установив курсор мыши в строке формул после слова ЕСЛИ перед открывающей скобкой:

В окно Значение_если_истина введем соответствующее выполнению условия значение Коэффициента, равное 1,2, а в Значение_если_ложь необходимо ввести вложенную функцию ЕСЛИ(), с целью дальнейшей проверки условий (условия 8 <= s < 10, при выполнении которого коэффициент k=1.8 и условия s= 10 при выполнении которого k=2.0)

После ввода значения ЕСЛИ(), необходимо вновь установить указатель мыши в строке формул, после второго ЕСЛИ перед открывающей скобкой. Будет вновь предложено окно для ввода аргументов функции ЕСЛИ(), на сей раз – первой вложенной. Как и в предыдущем случае, введем в окно Логического_значения функцию И(), перейдем в окно ввода аргументов уже для нее и в качестве аргументов введем – в качестве первого – С12>=8, в качестве второго С12<10:

и после возврата ко вводу аргументов второй функции ЕСЛИ()необходимо ввести значение коэффициента 1,8 в окно Значение_если_истина и еще одну функцию ЕСЛИ() в окно Значение_если_ложь

При вводе аргументов в третью вложенную функцию ЕСЛИ()условие формулируется проще C12=10, соответственно, нет необходимости в задействовании функции И(). В том случае, если данное условие выполняется, коэффициент равен 2, в том случае, если нет, то (с учетом того, что задействованы все возможные варианты значения среднего балла от 4 до 10 включительно) необходимо вывести текстовое значение «неправильные данные».

В итоге будет введена функция

=ЕСЛИ(И(C12>=4;C12<8);1,2;ЕСЛИ(И(C12>=8;C12<10);1,8;ЕСЛИ(C12=10;2;»неправильные данные»)))

в результате выполнения которой в ячейке D12 (коэффициент студента Макарова) будет выведено 1,2.

5.2 А после копирования значения функции в другие ячейки диапазона D12:D16, которые соответствуют значениям коэффициентов других студентов будет получена следующая таблица:

то есть у всех студентов значение коэффициента равно 1,2. Однако, например, если изменить оценку студента Макарова С.П. по предмету Информатика на 10, его средний балл превысит 8 и, соответственно, коэффициент повысится до 1,8:

6. Остается лишь по известному коэффициенту найти размер стипендии студента Макарова С.П. (просто умножив коэффициент на размер минимальной стипендии – пусть он будет равен 500), а затем, скопировав функцию в остальные ячейки – стипендий остальных студентов.

Для этого установим указатель мыши в ячейке E12 (Стипендия студента Макарова) и, перейдя в строку ввода в строке ввода формул введем =500*D12, то есть перемножим величину минимальной стипендии m (равной 500) на значение коэффициента студента. В результате получим, что стипендия студента Макарова равна 900 (тыс. руб.)

Скопируем данную формулу в диапазон E12:E16 и получим значения стипендий всех студентов.

Задание 3.

По результатам сдачи сессии группой студентов (таблица Итоги экзаменационной сессии), определить

— количество сдавших сессию на «отлично» (9 и 10 баллов);

— на «хорошо» и «отлично» (6-10 баллов);

— количество неуспевающих (имеющих 2 балла);

— самый «сложный» предмет;

— фамилию студента, с наивысшим средним баллом.

Выполнение.

Таблица Итоги экзаменационной сессии (ее можно просто скопировать на Лист Задание 3 с Листа Задание 2) имеет следующий вид:

Дополним таблицу двумя столбцами – Средний балл, в которую внесем Средний балл каждого из студентов и Минимальная оценка, в которую внесем минимальную оценку каждого из студентов, полученную во время сессии.

Сначала заполним ячейку Средний балл студента Макарова С.П. (ячейку F3), внеся в нее (например, с помощью кнопки Автосумма, выбрав функцию Среднее) формулу=СРЗНАЧ(C3:E3), с помощью которой вычисляется среднее из трех чисел (в данном случае – трех оценок).

Затем заполним ячейку Минимальная оценка студента Макарова С.П. (ячейку G3), внеся в нее (например, с помощью мастера функций, вызванного нажатием кнопки fx) формулу=МИН(C3:E3), с помощью которой будет определена минимальная из трех оценок, полученная этим студентом:

Далее выделим ячейки F3 и G3, подведем курсор мыши к правому нижнему углу ячейки G3 так, чтобы он принял вид маркера автозаполнения («черный крестик»), и, нажав на левую кнопку мыши скопируем содержимое ячеек F3 и G3 в диапазонF4:G7, где должны размещаться средние и минимальные оценки за сессию всех остальных студентов:

Затем определи количество студентов, (1) сдавших сессию на отлично (9 и 10 баллов), (2) на хорошо и отлично (6-10 баллов) и (3) количество неуспевающих студентов (имеющих 2 балла) и внесем результаты в ячейки E11, E12, E13 соответственно.

1. Очевидно, что у тех, кто сдал сессию на отлично средний балл будет больше либо равен 9. Таким образом, для определения количества отличников с использованием функции СЧЕТЕСЛИ() произведем подсчет количества таких студентов, то есть подсчет количества значений больших либо равных 9 в диапазоне F3:F7, в который внесены средние баллы студентов. Результат выполнения функции=СЧЁТЕСЛИ(F3:F7;»>=9″) внесем в ячейку E11.

2. Для подсчета количества сдавших сессию на «хорошо” и «отлично” воспользуемся столбцом Минимальная оценка. У таких студентов минимальная оценка будет больше либо равна 6. С использованием функции СЧЕТЕСЛИ() произведем подсчет количества таких студентов, то есть подсчет количества значений больших либо равных 6 в диапазонеG3:G7, в который внесена минимальная оценка, полученная каждым студентом за сессию. Результат выполнения функции=СЧЁТЕСЛИ(G3:G7;»>=6″) внесем в ячейку E12.

3. Для подсчета количества неуспевающих студентов вновь воспользуемся столбцом Минимальная оценка. У таких студентов минимальная оценка очевидно, будет больше либо равна 3. С использованием функции СЧЕТЕСЛИ() произведем подсчет количества таких студентов, то есть подсчет количества значений меньших либо равных 3 в диапазоне G3:G7, в который внесена минимальная оценка, полученная каждым студентом за сессию. Результат выполнения функции =СЧЁТЕСЛИ(G3:G7;»<=3″) внесем в ячейку E13:

Остается лишь определить (4) самый сложный предмет и (5) ФИО студента, получившего наивысший средний балл. Очевидно, что самым сложным предметом является тот, по которому средний балл, полученный студентами минимальный из трех возможных вариантов.

Минимальное число из нескольких можно определить с помощью функции Excel МИН(), в данном случае, эту функцию надо применить к диапазону данных C8:E8, в котором ранее подсчитаны средние баллы по предметам (=МИН(C8:E8)).

Остается лишь определить, какому из предметов будет соответствовать минимальная из трех средних оценок. Для этого внесем в ячейку E14 формулу =ЕСЛИ(C8=МИН(C8:E8);C2;ЕСЛИ(D8=МИН(C8:E8);D2;E2)) и при имеющихся исходных данных будет получен результат Математика.

Наконец, для определения (5) ФИО студента, получивший наивысший средний балл будут задействованы функции МАКС() (с помощью которой определяется максимальное из группы чисел) и опять же ЕСЛИ(). При определении необходимо последовательно сравнить максимальный из пяти возможных средний балл МАКС(F3:F7) со средним баллом каждого из пяти студентов, и в случае совпадения выдать в качестве результата фамилию этого студента.

Соответственно, будут задействованы 4 (на 1 меньше количества студентов) функции ЕСЛИ(), одна – внешняя и три вложенные. Результирующая формула будет иметь следующий вид:

=ЕСЛИ(F3=МАКС(F3:F7);B3;ЕСЛИ(F4=МАКС(F3:F7);B4;ЕСЛИ(F5=МАКС(F3:F7);B5;ЕСЛИ(F6=МАКС(F3:F7);B6;B7))))

В результате внесения данной функции в ячейку E15 будет получено следующее:

Задание 4.

Пусть в ячейках A1,A2,A3 записаны три числа, задающих длины сторон треугольника.

Написать формулу:

— определения типа треугольника (равносторонний, равнобедренный, разносторонний),

— определения типа треугольника (прямоугольный, остроугольный, тупоугольный),

— вычисления площади треугольника, если он существует. В противном случае в ячейку В6 вывести слово «нет».

1) Вариант формулы для определения типа треугольника (равносторонний, равнобедренный, разносторонний)

=ЕСЛИ(И(x+y>z;y+z>x;z+x>y);ЕСЛИ(И(z=x;y=x;z=y);»равосторонний»;ЕСЛИ(ИЛИ(x=z;z=y;x=y);»равнобедренный»;»разносторонний»));»не существует»)

2) Вариант формулы для определения типа треугольника (прямоугольный, остроугольный, тупоугольный)

=ЕСЛИ(И(x+y>z;y+z>x;x+z>y);ЕСЛИ((x^2+y^2-z^2)/(2*x*y)=0;»прямоугольный»;ЕСЛИ((x^2+y^2-z^2)/(2*x*y)>0;»остроугольный»;»тупоугольный»));»не существует»)

3) Вариант формулы для вычисления площади треугольника, если он существует

=ЕСЛИ(И(x+y>z;y+z>x;z+x>y);0,5*y*x*КОРЕНЬ(1-((x^2+y^2-z^2)/(2*x*y))^2);»не существует»)

Лабораторная работа №3_4. Построение графиков, поверхностей и диаграмм в Excel.

Задание 1.Составить таблицу расчета доходов фирмы в абсолютном и процентном отношении и диаграмму роста доходов на основе данных о доходах фирмы.

Выполнение.

1. Составить таблицу расчета доходов фирмы: определить тип, размер и стиль шрифтов для заголовков строк и столбцов: Times New Roman Cyr, размер 12, стиль полужирный; для остального текста — Times New Roman Cyr, размер 10, стиль обычный;

2. Вычислить рост уровня доходов фирмы в процентном отношении в каждом месяце 2013 года по отношению к январю 2013 года (3-й столбец таблицы);

=(Ci-C$3)/C$3 где Сi – адрес ячейки i-го месяца графы Уровень доходов фирмы в 2013 году, С$3 – абсолютный адрес ячейки Уровень доходов фирмы за январь 2013 года;

3. Вычислить суммарный уровень доходов фирмы за 2013 и 2012 годы, результаты поместить в последней строке второго и третьего столбца соответственно;

4. Вычислить среднее значение роста уровня доходов в процентах, результат поместить в последней строке четвертого столбца;

5. Построить диаграмму зависимости уровня доходов фирмы за 2013 и 2012 годы по месяцам в виде гистограммы;

6. Построить диаграмму зависимости уровня доходов фирмы в процентном отношении в виде линейного графика;

Задание 2. Составить круговую диаграмму с отображением среднего балла по предметам на основании таблицы «Итоги экзаменационной сессии» Лабораторной работы №3_3.

Какие установлены виды стипендий и каковы их размеры?

В РФ установлены различные виды стипендий, в том числе государственная социальная стипендия студентам. Порядок назначения и размер стипендий устанавливаются образовательным учреждением.

Государственная академическая стипендия

обучение осуществляется по очной форме обучения за счет федерального бюджета;
отсутствуют академическая задолженность и оценки «удовлетворительно» по итогам промежуточной аттестации (при этом с начала учебного года по месяц окончания первой промежуточной аттестации стипендия выплачивается всем студентам 1-го курса).

Конкретный размер стипендии учебное заведение определяет самостоятельно, однако он не может быть меньше установленных нормативов, которые могут быть проиндексированы с учетом уровня инфляции (ч. 8, 9, 10 ст. 36 Закона N 273-ФЗ; п. 1 Постановления Правительства РФ от 26.01.2017 N 88).

Также может быть назначена повышенная стипендия за особые достижения в какой-либо области деятельности (например, учебной, общественной, спортивной), а также если студент 1-го или 2-го курса в возрасте до 20 лет имеет только одного родителя — инвалида I группы (п. п. 6, 14 Порядка).

Государственная социальная стипендия

Данный вид стипендий назначается студентам, обучающимся по очной форме обучения за счет федерального бюджета, относящимся к одной из льготных категорий граждан, в том числе (п. 2 ч. 2, ч. 3, 5 ст. 36 Закона N 273-ФЗ; п. 13 Порядка):

являющимся детьми-сиротами и детьми, оставшимися без попечения родителей;
потерявшим в период обучения обоих родителей или единственного родителя;
являющимся детьми-инвалидами, инвалидами I и II групп, инвалидами с детства;
подвергшимся воздействию радиации вследствие катастрофы на Чернобыльской АЭС и иных радиационных катастроф;
являющимся инвалидами вследствие военной травмы или заболевания, полученных в период прохождения военной службы, и ветеранами боевых действий;
проходившим в течение не менее трех лет военную службу по контракту на воинских должностях, подлежащих замещению солдатами, матросами, сержантами, старшинами, и уволенным с военной службы по определенным основаниям, например по истечении срока контракта;
получившим государственную социальную помощь.

При этом нахождение студента в академическом отпуске, а также отпуске по беременности и родам, отпуске по уходу за ребенком до достижения им возраста трех лет не является основанием для прекращения выплаты стипендии (п. 23 Порядка).

Размер стипендии образовательное учреждение определяет самостоятельно, но он не может быть ниже установленных нормативов, которые могут быть проиндексированы с учетом уровня инфляции (ч. 8, 9, 10 ст. 36 Закона N 273-ФЗ; п. 1 Постановления Правительства РФ N 88).

Повышенная стипендия может быть назначена студентам 1-го и 2-го курса — отличникам и хорошистам либо студентам в возрасте до 20 лет, имеющим только одного родителя — инвалида I группы (п. 14 Порядка).

Обратите внимание!

В связи с коронавирусной инфекцией, если срок выплаты ранее назначенной государственной социальной стипендии истекает с 15 марта до 15 мая 2020 г. и подтверждение права на получение стипендии в электронном виде не представляется возможным, студентам обеспечивается выплата ежемесячной материальной поддержки не ниже размера социальной стипендии (п. п. 1.1, 1.2, 2 Приказа Минобрнауки России от 09.04.2020 N 566).

Государственные стипендии для аспирантов, ординаторов и ассистентов-стажеров

Данные стипендии назначаются аспирантам, ординаторам, ассистентам-стажерам, обучающимся по очной форме обучения за счет федерального бюджета, при отсутствии у них академической задолженности и оценок «удовлетворительно» по итогам промежуточной аттестации. При этом с начала учебного года по месяц окончания первой промежуточной аттестации стипендия выплачивается всем аспирантам, ординаторам, ассистентам-стажерам первого года обучения.

Размеры стипендий определяются образовательной организацией и не могут быть меньше установленных нормативов, которые могут быть проиндексированы с учетом уровня инфляции (п. 3 ч. 2, ч. 6, 8, 9, 10 ст. 36 Закона N 273-ФЗ; п. 15 Порядка; п. 1 Постановления Правительства РФ N 88).

Стипендии Президента РФ и стипендии Правительства РФ

Данные виды стипендий назначаются в размерах и порядке, утвержденных Президентом РФ или Правительством РФ (п. 4 ч. 2, ч. 12 ст. 36 Закона N 273-ФЗ).

стипендии студентам и аспирантам образовательных учреждений высшего профессионального образования, достигшим выдающихся успехов в учебе и научных исследованиях. Размер стипендии для студентов — 2 200 руб., для аспирантов — 4 500 руб.;
стипендии обучающимся очно по образовательным программам высшего образования по специальностям или направлениям подготовки, соответствующим приоритетным направлениям модернизации и технологического развития российской экономики. Стипендия назначается в том числе слушателям образовательных организаций, осуществляющих подготовку кадров в интересах обороны и безопасности государства, обеспечения законности и правопорядка. Размер стипендии для студентов (курсантов), слушателей — 7 000 руб., а для аспирантов (адъюнктов) — 14 000 руб.;
стипендии молодым (до 35 лет) ученым и аспирантам, осуществляющим перспективные научные исследования и разработки по приоритетным направлениям модернизации российской экономики. Размер стипендии — 22 800 руб.

К стипендиям Правительства РФ относятся, в частности, стипендии студентам (курсантам, слушателям) и аспирантам (адъюнктам), обучающимся очно по образовательным программам высшего образования по специальностям или направлениям подготовки, соответствующим приоритетным направлениям модернизации и технологического развития российской экономики. Размер стипендии для студентов (курсантов, слушателей) — 5 000 руб., для аспирантов (адъюнктов) — 10 000 руб. (п. п. 1, 2 Постановления Правительства РФ от 03.11.2015 N 1192).

Иные виды стипендий

именные стипендии, назначаемые органами государственной власти и местного самоуправления, юридическими и физическими лицами в размере и на условиях, определенных ими (например, стипендии Минобороны России для обучающихся в суворовском военном училище в размере 1 500 руб.);
стипендии обучающимся, назначаемые юридическими или физическими лицами, в том числе направившими их на обучение, в размере, определенном указанными лицами;
стипендии слушателям подготовительных отделений федеральных государственных вузов, обучающимся за счет федерального бюджета, в размере 2 000 руб.

Предусмотрена также выплата стипендий гражданам в период прохождения ими профессионального обучения и получения дополнительного профессионального образования по направлению органов службы занятости в порядке и размерах, установленных законодательством (ст. 29 Закона от 19.04.1991 N 1032-1).

«Электронный журнал «Азбука права», актуально на 25.06.2020

Другие материалы журнала «Азбука права» ищите в системе КонсультантПлюс.

Наиболее популярные материалы «Азбуки права» доступны в мобильном приложении КонсультантПлюс: Студент.