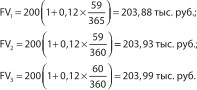Формула fv
Содержание
- Наращение по простым процентам
- Дисконтирование по простым процентам
- Определение процентной ставки и срока проведения операции
- Эквивалентность процентных ставок r и d
- Наращение по сложным процентам
- Дисконтирование по сложным процентам
- Использование сложной учетной ставки
- Вывод
- 9.1Операции наращения и дисконтирования
Наращение может осуществляться по схеме простых и сложных процентов.

Формула наращения простых процентов (simple interest). Наращение простых процентов означает, что инвестируемая сумма ежегодно возрастает на величину PV • r. В этом случае размер инвестированного капитала через n лет можно определить по формуле:
FV = PV (1 + r • n).
Формула наращения сложных процентов (compound interest). Наращение по схеме сложных процентов означает, что очередной годовой доход исчисляется не с исходной величины инвестированного капитала, а с общей суммы, включающей также ранее начисленные и не востребованные инвестором проценты. В этом случае размер инвестированного капитала через n лет можно определить по формуле:
FV = PV (1 + r)n.
При одном и том же значении процентной ставки:
1) темпы наращения сложных процентов выше темпов наращения простых, если период наращения превышает стандартный интервал начисления дохода;
2) темпы наращения сложных процентов меньше темпов наращения простых, если период наращения меньше стандартного интервала начисления дохода.
Области применения простых и сложных процентов. Простые и сложные проценты могут применяться как в отдельных операциях, так и одновременно. Области применения простых и сложных процентов можно разделить на три группы:
1) операции с применением простых процентов;
2) операции с применением сложных процентов;
3) операции с одновременным применением простых и сложных процентов.
1. Областью применения простых процентов чаще всего являются краткосрочные операции (со сроком до одного года) с однократным начислением процентов (краткосрочные ссуды, вексельные кредиты) и реже — долгосрочные операции.

При краткосрочных операциях используется так называемая промежуточная процентная ставка, под которой понимается годовая процентная ставка, приведенная к сроку вложения денежных средств. Математически промежуточная процентная ставка равна доле годовой процентной ставки. Формула наращения простых процентов с использованием промежуточной процентной ставки имеет следующий вид:
FV = PV (1 + f • r),
или
FV = PV (1 + t • r / Т),
где f=t/T;
t — срок вложения денежных средств (при этом день вложения и день изъятия денежных средств принимаются за один день); Т — расчетное количество дней в году.
При долгосрочных операциях начисление простых процентов рассчитывается по формуле:
FV = PV (1 + r • n),
где n — срок вложения денежных средств (в годах). ,
2. Областью применения сложных процентов являются долгосрочные операции ( со сроком, превышающим год), в том числе предполагающие внутригодовое начисление процентов.

В первом случае применяется обычная формула начисления сложных процентов:
FV = PV (1 + r)n.
Во втором случае применяется формула начисления сложных процентов с учетом внутригодового начисления. Под внутригодовым начислением процентов понимается выплата процентного дохода более одного раза в год. В зависимости от количества выплат дохода в год (m) внутригодовое начисление может быть:
1) полугодовым (m = 2);
2) поквартальным (m = 4);
3) ежемесячным (m = 12);
4) ежедневным (m = 365 или 366);
5) непрерывным (m -» ?).
Формула наращения при полугодовом, поквартальном, ежемесячном и ежедневном начислении сложных процентов имеет следующий вид:
FV = PV (1 + r / m)nm,
где PV — исходная сумма;
г — годовая процентная ставка;
n — количество лет;
m — количество внутригодовых начислений;
FV — наращенная сумма.
Процентный доход при непрерывном начислении процентов рассчитывается по следующей формуле:

FVn = Р • ern,
или:
FVn = P • e?n,
где: e = 2, 718281 — трансцендентное число (число Эйлера);
е?n — множитель наращения, который используется как при целом, так и дробном значении n;
? — специальное обозначение процентной ставки при непрерывном начислении процентов (непрерывная процентная ставка, «сила роста»);
n — количество лет.
При одинаковой величине исходной суммы, одинаковом сроке вложения денежных средств и значении процентной ставки возвращаемая сумма оказывается больше в случае использования формулы внутригодовых начислений, чем в случае использования обычной формулы начисления сложных процентов:
FV = PV (1 + r / m)nm > FV = PV (1 + r)n.
Если доход, полученный при использовании внутригодовых начислений, выразить в процентах, то полученная процентная ставка окажется выше той, которая использовалась при обычном начислении сложных процентов.
Таким образом, первоначально заявленная годовая процентная ставка для начисления сложных процентов, называемая номинальной, не отражает реальной эффективности сделки. Процентная ставка, отражающая фактически полученный доход, называется эффективной. Классификацию процентных ставок при внутригодовом начислении сложных процентов наглядно иллюстрирует рисунок.

Номинальная процентная ставка задается изначально. Для каждой номинальной процентной ставки и на ее основании можно рассчитать эффективную процентную ставку (rе).
Из формулы наращения сложных процентов можно получить формулу эффективной процентной ставки:
FV = PV (1 + r)n;
(1 + re) = FV / PV.
Приведем формулу наращения сложных процентов с внутригодовыми начислениями, при которых каждый год начисляется r / m процента:
FV = PV (1 + r / m)nm.
Тогда эффективная процентная ставка находится по формуле:
(1 + re) = (1 + r/m)m,
или
re = (l + r/m)m- 1,
где rе — эффективная процентная ставка; r — номинальная процентная ставка; m — количество внутригодовых выплат.
Величина эффективной процентной ставки зависит от количества внутригодовых начислений (m):
1) при m = 1 номинальная и эффективная процентные ставки равны;
2) чем больше количество внутригодовых начислений (значение m), тем больше эффективная процентная ставка.
Областью одновременного применения простых и сложных процентов являются долгосрочные операции, срок которых составляет дробное количество лет. При этом начисление процентов возможно двумя способами:
1) начисление сложных процентов с дробным числом лет;
2) начисление процентов по смешанной схеме.
В первом случае для расчетов применяется формула сложных процентов, в которой присутствует возведение в дробную степень:
В финансовой практике часто приходится решать задачу, обратную вычислению наращенной суммы, которая может быть сформулирована таким образом: определить сумму 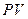 , которую необходимо инвестировать в данный момент времени, с тем, чтобы через некоторый определенный период
, которую необходимо инвестировать в данный момент времени, с тем, чтобы через некоторый определенный период 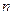 получить при установленной ставке процента
получить при установленной ставке процента 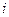 требуемую наращенную сумму
требуемую наращенную сумму 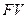 . Для решения этой задачи применяется операция дисконтирования.
. Для решения этой задачи применяется операция дисконтирования.
Дисконтирование позволяет по известным наращенной сумме, процентной ставке и сроке финансовой операции определить современную стоимость этой наращенной суммы.
Другими словами дисконтирование позволяет определить, какую первоначальную сумму надо дать в долг, чтобы получить в конце срока сумму 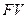 при условии, что на долг начисляются проценты по ставке
при условии, что на долг начисляются проценты по ставке 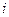 .
.
В зависимости от вида процентной ставки применяются два вида дисконтирования: математическое дисконтирование и банковский (коммерческий) учет. В первом случае при расчете применяют обычные (декурсивные), а во втором – авансовые проценты.
Рассмотрим, как производится математическое дисконтирование.
Выразив из формулы (2.1) 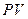 , получим формулу математического дисконтирования:
, получим формулу математического дисконтирования:
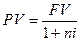 ,(2.5)
,(2.5)
Здесь — современная стоимость наращенной (будущей) суммы денег ; — срок проведения финансовой операции (число процентных периодов); — процентная ставка.
Дисконтный множитель показывает, какую долю составляет первоначальная величина долга в его окончательной сумме .
Пример. Заемщик должен возвратить кредит единовременным платежом с процентами за период 2 года. Проценты по кредиту составили 12% годовых. Какую сумму получил заемщик в момент заключения кредитного договора и чему равен дисконт, если сумма к возврату составляет 1 500 000 рублей?
Решение: FV=1500 000 рублей; n=2 года; i= 0,12
,
В случае если срок финансовой операции задан в днях или в месяцах, из формулы (2.2) получим формулу математического дисконтирования для <1:
Большинство хозяйственных операций (приобретение основных средств, покупка/продажа ценных бумаг, лизинг, получение/погашение банковских кредитов, анализ инвестиционных проектов и др.) порождают денежные потоки. Осуществление этих операций сопровождается множеством выплат и поступлений денежных средств, образуя денежный поток, распределенный во времени.
В связи с этим в процессе управления финансами предприятия возникает необходимость в проведении специальных расчетов, связанных с движением денежных потоков в различные периоды времени. Ключевую роль в этих расчетах играет оценка стоимости денег во времени. Концепция такой оценки базируется на том, что стоимость денег с течением времени изменяется с учетом нормы прибыли, сложившейся на финансовом рынке, в качестве которой выступает ставка ссудного процента или норма доходности по государственным ценным бумагам.
Из принципа временной стоимости денег (Time Value of Money, TVM) вытекает два важных следствия:
- необходимость учета фактора времени, в особенности при проведении долгосрочных финансовых операций;
- некорректность суммирования денежных величин, относящихся к разным периодам времени.
Рассмотрим отдельные элементы методического инструментария стоимости денег.
Процент — сумма дохода от предоставления капитала в долг или плата за пользование ссудным капиталом во всех его формах (депозитный и кредитный процент, по облигациям и векселям).
Простой процент — сумма дохода, начисляемого к основной сумме капитала в каждом интервале, по которой дальнейшие расчеты не производят.
Сложный процент — сумма дохода, начисляемого в каждом интервале, которую не выплачивают, а присоединяют к основной сумме капитала (вклада) в последующем платежном периоде.
Процентная ставка — удельный показатель, в соответствии с которым в установленные сроки выплачивают сумму процентов в расчете на единицу капитала (вклада). На практике процентная ставка выражает соотношение годовой суммы процентного дохода к объему основного долга.
Будущая стоимость денег (Future Value, FV) — сумма вложенных в настоящий момент денежных средств, в которую они превратятся через определенный период времени с учетом выбранной процентной ставки.
Настоящая стоимость денег (Present Value, PV) — сумма будущих денежных средств (вклада), приведенных с учетом конкретной процентной ставки к настоящему моменту времени.
Наращение стоимости (компаундинг — compounding) — процесс пересчета настоящей стоимости денежных средств (вклада) в их будущую стоимость в конкретном периоде времени путем добавления к первоначальной сумме начисленной величины процента.
Дисконтирование стоимости (discounting) — процесс приведения будущей стоимости денежных средств (вклада) к их настоящей стоимости путем исключения из будущей суммы соответствующей величины процента (дисконта). Посредством такой финансовой операции достигают сопоставимости текущей стоимости предстоящих денежных потоков.
Период начисления — общий период времени, в течение которого осуществляют процесс наращения или дисконтирования денежной суммы (вклада).
Интервал начисления – это минимальный период, по прошествии которого происходит начисление процентов.
Декурсивный способ начисления процентов — способ, при котором проценты начисляются в конце каждого интервала начисления. Их величина определяется исходя из величины предоставляемого капитала. Соответственно, декурсивная процентная ставка представляет собой выраженное в процентах отношение суммы начисленного за определенный интервал дохода к сумме, имеющейся на начало данного интервала.
Антисипативный способ (предварительный) начисления процентов — это способ, при котором проценты начисляются в начале каждого интервала начисления. Сумма процентных денег определяется исходя из наращенной суммы. Процентной ставкой будет выраженное в процентах отношение суммы дохода, выплачиваемого за определенный интервал, к величине наращенной суммы, полученной по прошествии этого интервала. Определяемая таким способом процентная ставка называется учетной ставкой, или антисипативным процентом.
Наращение по простым процентам
Простые проценты используются в краткосрочных финансовых операциях, срок проведения которых меньше года или равен ему.
Наращение по годовой ставке простых процентов осуществляется по формуле:
FV = PV(1 + r × n), (1)
где FV — будущая стоимость;
PV — первоначальная стоимость;
n — число периодов (лет);
r — процентная ставка.
Пример 1
Клиент сделал вклад в банк в сумме 10 000 руб. под 12% годовых сроком на пять лет. По формуле (1) находим:
FV = 10 000(1 + 0,12 × 5) = 16 000 руб.
Сумма начисленных процентов составит 6000 руб. (16 000 – 10 000).
Если продолжительность краткосрочной операции выражена в днях, то срок ее проведения корректируется следующим образом:
n = t / B, (2)
где t — число дней проведения операции;
В — временная база (число календарных дней в году).
Тогда будущую стоимость операции можно определить:
(3)
Время вклада (ссуды) может вычисляться или с учетом точного числа в месяцах, или при допущении, что расчетная продолжительность любого месяца равна 30 дням.
В результате конкретные расчеты по начислению процентов могут вестись по трем вариантам:
365/365 — точное число дней проведения операции и фактическое число дней в году (точные проценты);
365/360 — точное число дней проведения операции и финансовый год (12 месяцев по 30 дней);
360/360 — приближенное число дней проведения операции (месяц принимается равным 30 дням) и финансовый год (обыкновенные проценты).
Для одних и тех же условий начисления процентов проведение расчетов по этим вариантам приводит к несколько отличающимся финансовым последствиям.
Пример 2
Акционерное общество получило в банке ссуду в размере 200 тыс. руб. под 15% годовых на срок с 15 февраля до 15 апреля. Определить сумму, которую необходимо возвратить банку.
Сначала нужно определить число дней использования ссуды: 15 февраля – 46-й день в году, 15 апреля – 105-й день в году. Отсюда точный срок ссуды – 59 дней. Тогда, по формуле (3) находим:
Дисконтирование по простым процентам
Существует два способа дисконтирования.
Математическое дисконтирование — способ, основанный на решении задачи, обратной определению будущей стоимости. При проведении расчетов здесь используется процентная ставка.
С учетом принятых ранее обозначений формула дисконтирования по ставке r будет иметь вид:
(4)
Доход банка (FV – PV) называют дисконтом, а используемую норму приведения r — декурсивной ставкой процентов.
Пример 3
Какую цену заплатит инвестор за бескупонную облигацию, номинальная стоимость которой 500 тыс. руб., а срок погашения — 270 дней, если требуемая норма доходности — 20%?
По формуле (4) при использовании обыкновенных процентов:
PV = 500 / (1 + 0,2 × 270 / 360) = 434,78 тыс. руб.;
точных процентов:
PV = 500 / (1 + 0,2 × 270 / 365) = 435,56 тыс. руб.
Банковское дисконтирование применяется при банковском учете векселей, при этом проценты начисляются на сумму, подлежащую уплате в конце срока операции. При проведении расчетов используется учетная ставка d:
(5)
При дисконтировании по учетной ставке чаще всего используют временную базу 360/360 или 360/365. Используемую при этом норму приведения d называют антисипативной ставкой процентов.
Пример 4
Простой вексель на сумму 500 тыс. руб. со сроком погашения один год учитывается в банке через 270 дней по простой учетной ставке 20%. Какую сумму получит владелец векселя?
Используем формулу (5), учитывая, что n — это разность во времени между моментом учета и сроком погашения векселя:
PV = 500 (1 – 0,2 × 90 / 360) = 475 тыс. руб.
Применение двух рассмотренных методов дисконтирования к одной и той же сумме приводит к разным результатам, даже при r = d. Учетная ставка дает более быстрое снижение суммы, чем обычная.
Пример 5
Простой вексель на сумму 100 тыс. руб. с оплатой через 90 дней учитывается в банке немедленно после получения. Необходимо определить сумму, полученную владельцем векселя при процентной/учетной ставке 15%.
При использовании процентной ставки по формуле (4):
PV = 100 / (1 + 0,15 × 90 / 360) = 96,39 тыс. руб.
При использовании учетной ставки по формуле (5):
PV = 100 (1 – 0,15 × 90 / 360) = 96,25 тыс. руб.
Учетная ставка d применяется и для наращения по простым процентам (например, при определении будущей суммы контракта):
(6)
Изменим условия примера 5 следующим образом.
Пример 6
На какую сумму должен быть выписан вексель, чтобы поставщик, проведя операцию учета, получил стоимость товаров (100 тыс. руб.) в полном объеме, если учетная ставка — 15%?
По формуле (6) определяем будущую стоимость (номинал) векселя:
FV = 100 / (1 – 0,15 × 90 / 360) = 103,896 тыс. руб.
Определение процентной ставки и срока проведения операции
Величина процентной ставки r или учетной ставки d может быть определена из соотношений (1) и (5):
(7)
(8)
Пример 7
Краткосрочное обязательство со сроком погашения 90 дней было приобретено по цене 98,22 ед. от номинала. Необходимо определить доходность операции для инвестора.
Она составляет (с использованием обыкновенных процентов):
Срок операции в днях определяется следующим образом:
(9)
(10)
Пример 8
Необходимо определить срок владения обязательством стоимостью 98,22 ед., погашаемого по номиналу, если требуемая норма доходности 7,2%.
Эквивалентность процентных ставок r и d
Эквивалентные процентные ставки — это такие ставки разного вида, применение которых при одинаковых начальных условиях дает одинаковые финансовые результаты.
Эквивалентные процентные ставки необходимо знать в случаях, когда существует возможность выбора условий финансовой операции и требуется инструмент для корректного сравнения различных процентных ставок.
Вывод формул эквивалентности базируется на равенстве соответствующих множителей наращения:
1 + n × r = (1 – n × d) – 1. (11)
С учетом формулы (11) для операций с продолжительностью менее года соотношения эквивалентности примут вид:
временная база одинакова и равна В (360 или 365 дней):
(12)
(13)
временная база ставки r равна 365 дням, а d — 360 дням:
(14)
(15)
Пример 9
Срок уплаты по векселю — 250 дней. При этом ставка простых процентов измеряется при временной базе 365 дней, а простая учетная ставка — при временной базе 360 дней. Какова будет доходность, измеренная в виде ставки простых процентов, учета векселя по простой учетной ставке 10%?
Используя формулу (14) для r при заданных временных базах, получим:
r = 365 × 0,1 / (360 – 250 × 0,1) = 0,1089, или 10,89%.
Допустим, что настоящая стоимость векселя — 100 000 руб. Тогда его номинальная стоимость по формуле (3) составит:
Учет векселя за 250 дней позволит рассчитать по формуле (5) его настоящую стоимость:
Наращение по сложным процентам
Сложные проценты применяются, как правило, в финансовых операциях, срок проведения которых более года. При этом базой исчисления процентов является как исходная сумма финансовой операции, так и сумма уже накопленных к этому времени процентов.
Наращение по сложным процентам имеет вид:
FVn = PV (1 + r)n. (16)
Наращение по сложным процентам подразумевает реинвестирование полученных доходов или капитализацию.
Начисление сложных процентов может осуществляться не один, а несколько раз в году. В этом случае оговаривается номинальная ставка процентов j — годовая ставка, по которой определяется величина ставки процентов, применяемая на каждом интервале начисления.
При m равных интервалах начисления и номинальной процентной ставке j эта величина считается равной j / m. Тогда, если срок финансовой операции составляет n лет, выражение для определения наращенной суммы (16) примет вид:
(17)
При увеличении числа периодов начисления m будущая величина FVmn также возрастает.
Пример 10
Первоначальная сумма вложения 200 тыс. руб. Определить наращенную сумму через пять лет при использовании сложной ставки процентов в размере 28% годовых. Решить пример для случаев, когда проценты начисляются по полугодиям, поквартально.
По формуле (16) для сложных процентных ставок:
FV = 200(1 + 0,28)5 = 687,2 тыс. руб.
По формуле (17) для начисления по полугодиям:
FV = 200(1 + 0,28 / 2)10 = 741,4 тыс. руб.
По той же формуле для поквартального начисления:
FV = 200(1 + 0,28 / 4)20 = 773,9 тыс. руб.
Если срок финансовой операции n в годах не является целым числом, множитель наращения k определяется по формуле:
k = (1 + r)na (1 + nb × r), (18)
где n = na + nb;
na — целое число лет;
nb — оставшаяся дробная часть года.
На практике в данном случае часто применяют формулу (16) с соответствующим нецелым показателем степени. Однако этот способ является приблизительным. Чем больше значения входящих в формулу величин, тем погрешность при вычислениях будет больше.
Пример 11
Первоначальная сумма долга равна 50 000 тыс. руб. Необходимо определить наращенную сумму через 2,5 года, используя два способа начисления сложных процентов по ставке 25% годовых.
По формуле (18) получаем:
FV = 50 000(1 + 0,25)2 (1 + 0,5 × 0,25) = 87 890,6 тыс. руб.
Для второго способа используем формулу (16) с нецелым показателем степени:
FV = 50 000(1 + 0,25)2,5 = 87 346,4 тыс. руб.
При использовании приблизительного метода упущенная выгода могла бы составить около 550 тыс. руб.
Если начисление сложных процентов осуществляется несколько раз в году и общее число интервалов начисления не является целым числом (mn — целое число интервалов начисления, l — часть интервала начисления), то выражение (17) принимает вид:
(19)
Для целого числа периодов начисления используется формула сложных процентов (16), а для оставшейся части — формула простых процентов (1).
На практике часто возникает необходимость сравнения условий финансовых операций, предусматривающих различные периоды начисления процентов. В этом случае соответствующие процентные ставки приводят к их годовому эквиваленту по формуле:
(20)
Полученную при этом величину называют эффективной процентной ставкой (effective percentage rate — EPR), или ставкой сравнения.
Пример 12
На четырехлетний депозит в 10 000 руб. производится ежеквартальное начисление сложных процентов по ставке 2,5%, то есть из расчета 10% годовых. Будет ли эквивалентной инвестицией депозит в 10 000 руб., вложенный на тот же срок под 10%, начисляемых один раз в год?
Рассчитаем эффективную ставку для обеих операций:
ежеквартально: EPR = (1 + 0,1 / 4)4 – 1 = 0,103813;
ежегодно: EPR = (1 + 0,1 / 1)1 – 1 = 0,10.
Таким образом, условия помещения суммы в 10 000 руб. на депозит сроком на четыре года под 2,5%, начисляемых ежеквартально, будут эквивалентными годовой ставке, равной 10,3813%. Следовательно, первая операция более выгодна для инвестора.
Если известна величина EPR, номинальная ставка процентов может быть определена следующим образом:
(21)
Дисконтирование по сложным процентам
Рассмотрим использование при математическом дисконтировании сложных процентных ставок:
(22)
Если проценты будут начисляться m раз в году, то формула (22) примет вид:
(23)
Пример 13
Банк производит начисление процентов на внесенную сумму по сложной процентной ставке, равной 20% в год. Какую сумму следует положить на депозит при условии, что вкладчик рассчитывает получить 10 000 тыс. руб. через 10 лет? Требуется рассмотреть два варианта начисления процентов — ежегодное и ежеквартальное.
При ежегодном начислении процентов по формуле (22):
PV = 10 000 / (1 + 0,2)10 = 1615,1 тыс. руб.
При ежеквартальном начислении процентов по формуле (23):
PV = 10 000 / (1 + 0,2 / 4)40 = 1420,5 тыс. руб.
Использование сложной учетной ставки
Для расчета операции дисконтирования по сложной учетной ставке используется формула:
PVn = FVn(1 – d)n. (24)
Пример 14
Владелец векселя номинальной стоимостью 500 тыс. руб. и периодом обращения 1,5 года предложил его банку сразу для учета, то есть за 1,5 года до погашения. Банк согласился учесть вексель по сложной учетной ставке 20% годовых. Требуется определить дисконт, полученный банком, и сумму, выданную владельцу векселя.
Используя формулу (24), находим:
PV = 500 (1 – 0,2)1,5 = 357,77 тыс. руб.
Дисконт банка составит: 500 – 357,77 = 142,23 тыс. руб.
Для данных условий определим сумму, которую получил бы владелец векселя, если бы банк произвел учет векселя по простой учетной ставке 20%. Для этого используем формулу (5):
PV = 500 (1 – 0,2 × 1,5) = 350 тыс. руб.
Дисконт банка составит 500 – 350 = 150 тыс. руб.
Таким образом, банку выгоднее учитывать вексель по простой учетной ставке.
Если дисконтирование по сложной учетной ставке производится m раз в году, расчетная формула будет иметь следующий вид:
(25)
Пример 15
Сохраним условия предыдущего примера, но пусть расчет дисконтирования производится ежеквартально, то есть m = 4.
По формуле (25) получим:
PV = 500 (1 – 0,2 / 4)6 = 367,55 тыс. руб.
Дисконт банка составит: 500 – 367,55 = 132,45 тыс. руб.
Доход банка при ежеквартальном дисконтировании будет меньше, чем при ежегодном дисконтировании, на: 142,23 – 132,45 = 9,78 тыс. руб.
При дисконтировании с начислением процентов за периоды менее года может использоваться понятие «эффективная сложная учетная ставка». Эффективная сложная учетная ставка, эквивалентная сложной учетной ставке при заданном значении m, определяется по формуле:
dэф = 1 – (1 – d / m)m. (26)
Пример 16
Долговое обязательство номинальной стоимостью 500 тыс. руб. должно быть погашено через пять лет. Сложная учетная ставка равна 20% годовых. Начисление процентов ежеквартальное. Требуется определить настоящую величину стоимости обязательства и эффективную учетную ставку.
Используя формулы (25) и (26), получим:
PV = 500 (1 – 0,2 / 4)20 = 179,243 тыс. руб.
dэф = 1 – (1 – 0,2 / 4)4 = 0,18549, или 18,549%.
Подставив значение 18,549% в формулу (24), получим:
PV = 500 (1 – 0,18549)5 = 179,247 тыс. руб.
Расхождение между величинами настоящей суммы, рассчитанными по этим формулам, находятся в пределах точности расчета.
При известных величинах FV, PV и n процентную ставку можно определить по формуле:
(27)
Пример 17
Сумма в 10 000 руб., помещенная в банк на четыре года, составила величину 14 641 руб. Необходимо определить доходность операции.
По формуле (27) находим:
r = (14 641 / 10 000)1/4 – 1 = 0,1, или 10%.
Длительность операции определяется логарифмированием:
(28)
Пример 18
Сумма в 10 000 руб., помещенная в банк под 10% годовых, составила величину в 14 641 руб. Необходимо определить срок проведения операции.
По формуле (28) находим:
n = log (14 641 / 10 000) / log (1 + 0,1) = 4 года.
Вывод
Приведенные расчетные формулы описывают механизм влияния фактора времени на результат финансовых операций. Их использование позволит избежать ошибок и потерь в условиях снижения покупательной способности денег.
Данная публикация размещена в «Энциклопедии менеджера E-xecutive.ru» в рамках сотрудничества с проектом www.cfin.ru
На портале www.cfin.ru она расположена
Д.В. Арутюнова
Инновационный менеджмент
Учебное пособие. – Ростов-на-Дону: Изд-во ЮФУ, 2014. – 152 с.
Предыдущая
9.1Операции наращения и дисконтирования
Простейшим видом финансовой сделки является однократное предоставление в долг некоторой суммы PV с условием, что через некоторое время t будет возвращена большая сумма FV. Как известно, результативность подобной сделки может быть охарактеризована двояко: либо с помощью абсолютного показателя — прироста (FV — PV), либо путем расчета некоторого относительно показателя. Абсолютные показатели чаще всего не подходят для подобной оценки ввиду их несопоставимости в пространственно-временном аспекте. Поэтому пользуются специальным коэффициентом — ставкой.
Этот показатель рассчитывается отношением приращения исходной суммы к базовой величине, в качестве которой можно брать либо PV либо FV. Таким образом, ставка рассчитывается по одной из двух формул:
темп прироста («процентная ставка», «процент», «рост», «ставка процента», «норма прибыли», «доходность»)
темп снижения (учетная ставка», «дисконт», «коэффициент дисконтирования»)
Очевидно, что обе ставки взаимосвязаны, т.е. зная один показатель, можно рассчитать другой:
Оба показателя могут выражаться либо в долях единицы, либо в процентах. Различие в этих формулах состоит в том, какая величина берется за базу сравнения: в формуле (Матем. 1) — исходная сумма, в формуле (Матем. 2) — возвращаемая сумма.
Очевидно, что r t > d t, а степень расхождения зависит от уровня процентных ставок, имеющих место в конкретный момент времени.
В прогнозных расчетах, например, при оценке инвестиционных проектов, как правило имеют дело с процентной ставкой, хотя обычно это не оговаривается. Объяснение этому может быть, например, таким.
1) Во-первых, анализ инвестиционных проектов, основанный на формализованных алгоритмах, может выполняться лишь в относительно стабильной экономике, когда уровни процентных ставок невелики и сравнительно предсказуемы в том смысле, что их значения не могут измениться в несколько раз или на порядок. Если вероятна значительная вариабельность процентных ставок, должны применяться другие методы анализа и принятия решений, основанные, главным образом, на неформализованных критериях. При разумных значениях ставок расхождения между процентной и дисконтной ставками, как мы видели, относительно невелики и потому в прогнозных расчетах вполне может быть использована любая из них.
2) Во-вторых, прогнозные расчеты не требуют какой-то повышенной точности, поскольку результатами таких расчетов являются ориентиры, а не «точные» оценки. Поэтому, исходя из логики подобных расчетов, предполагающих их многовариантность, а также использование вероятностных оценок и имитационных моделей, излишняя точность не требуется.
Итак, в любой простейшей финансовой сделке всегда присутствуют три величины, две из которых заданы, а одна является искомой.
Процесс, в котором заданы исходная сумма и процентная ставка, в финансовых вычислениях называется процессом наращения. Процесс, в котором заданы ожидаемая в будущем к получению (возвращаемая) сумма и коэффициент дисконтирования, называется процессом дисконтирования. В первом случае речь идет о движении денежного потока от настоящего к будущему, во втором — о движении от будущего к настоящему (см. рис.).
Экономический смысл финансовой операции, задаваемой формулой (Матем. 1), состоит в определении величины той суммы, которой будет или желает располагать инвестор по окончании этой операции. Поскольку из формулы (Матем. 1):
то видно, что время генерирует деньги.
Величина FV показывает как бы будущую стоимость «сегодняшней» величины PV при заданном уровне доходности.
Экономический смысл дисконтирования заключается во временном упорядочении денежных потоков различных временных периодов. Коэффициент дисконтирования показывает, какой ежегодный процент возврата хочет (или может) иметь инвестор на инвестируемый им капитал. В этом случае искомая величина PV показывает как бы текущую, «сегодняшнюю» стоимость будущей величины FV.
Предыдущая
Будущая стоимость — англ. Future Value, является суммой, в которую на определенную дату в будущем превратится определенная сумма денег, инвестированная сегодня под заранее известную процентную ставку. Она рассчитывается на базе концепции стоимости денег во времени, основываясь на процентных ставках и настоящей стоимости. Будущая стоимость инвестиций зависит от того, каким методом начисляются проценты: простые проценты, сложные проценты или аннуитет.
Идея, лежащая в основе концепции будущей стоимости денег, состоит в том, что $1000 сегодня стоят больше, чем $1000 через год. Так происходит потому что деньги могут быть помещены на сберегательный счет или размещены в форме других инвестиций, а, следовательно, принесут доход в течение года. Это называют концепцией стоимости денег во времени, которая применяется во многих инвестиционных схемах от сберегательных счетов, до индивидуальных пенсионных планов.
При начислении простых процентов формула для расчета будущей стоимости (FV) инвестиций имеет следующий вид:
где PV — настоящая стоимость (сумма, которая инвестируется в настоящий момент);
i — процентная ставка за период начисления процентов (например, если проценты начисляются раз в год, то годовая; если проценты начисляются ежемесячно, то за месяц);
t – количество периодов времени, в течение которого начисляются проценты (например, если проценты начисляются ежемесячно, а деньги инвестируются на 1,5 года, то t составит 18, то есть 18 месяцев в течение которых будут начисляться проценты).
По многим видам инвестиций начисляются сложные проценты. В этом случае формула для расчета их будущей стоимости имеет следующий вид:
Например, если первоначальная сумма инвестиций составляет $2000, процентная ставка 7% годовых, начисление процентов осуществляется ежемесячно, а инвестиционный горизонт составляет 3года, то будущая стоимость составит:
FV = 5000 * (1 +0,07/12)36 = $6164,63
Это означает, что $5000 сегодня будут стоить $6164,63 через три года при условии ежемесячного начисления процентов по ставке 7% годовых.
Однако процентные ставки могут колебаться, причем существенно. Например, если они возрастут до 11% годовых, то новый инвестор, который осуществит аналогичную инвестицию, через три года получит сумму равную:
FV = 5000 * (1 +0,11/12)36 = $6944,39
При этом инвестиции, осуществленные ранее под 7%, станут менее привлекательными, и их продажа станет возможной только с дисконтом. Напротив, если процентные ставки упадут ниже 7% годовых, новые инвестиции будут менее привлекательными. Поэтому продажа старых инвестиций будет осуществляться выше номинальной стоимости, то есть с премией.
Аннуитеты являются финансовыми продуктами, которые обеспечивают регулярные выплаты по фиксированной процентной ставке. Самыми простыми формами аннуитетов являются регулярное внесение средств на сберегательный счет, по которому проценты выплачиваются ежемесячно, или ипотека с ежемесячными платежами, включающими принципал и проценты. Для расчета будущей стоимости аннуитета используется следующая формула:
где A – размер платежа при аннуитете.
Примером аннуитетов может служить пожизненный аннуитет. По сути, он является средствами, которые накапливаются за счет регулярного внесения платежей клиентом в течение определенного периода времени, а затем начинают выплачиваться в виде стабильного потока доходов, обычно после выхода клиента на пенсию. При оценке стоимости пожизненного аннуитета тщательно оценивается его будущая стоимость, а также учитываются такие факторы, как пенсионный возраст и процентные ставки.